3D Polynomial Trend Modeling
This interpolation method best-fits first through third order polynomial equations to the observed data. These polynomial equations are then used to define predicted g-values for the solid model voxel nodes.
3D Polynomial Trend Modeling fits 1st, 2nd, and 3rd-order polynomials to XYZG data. Trend polynomials have five uses;
(1) determining and projecting the overall trend of XYZG data,
(2) biasing/enhancing other algorithms along a trend,
(3) spatially limiting the interpolations of other algorithms,
(4) projecting models outside the areas of control, and
(5) identifying data residuals that deviate from the overall trend (i.e., anomalies and bad data).
First-order models are typically planar gradients (Figure 1). First-order polynomial models are seldom used.
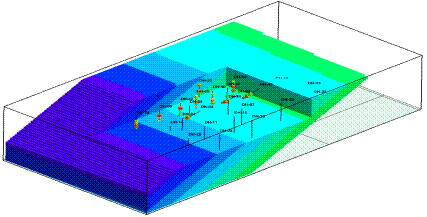
Figure 1. First-Order 3D Trend Polynomial Model
Second-order models are typically ovoids (Figure 2). Second-order polynomials are useful for identifying trends in groundwater contamination plumes, mineralization zones, hydrothermal gradients, etc.

Figure 2. Second-Order 3D Trend Polynomial Model
Third-order models are typically bent, pinched, or flared ovoids (Figure 3 & Figure 4). Third-order polynomials tend to be more erratic and “inventive” than second-order polynomials.

Figure 3. Third-Order 3D Trend Polynomial Model Suggesting an Off-Site Source of Groundwater Contamination
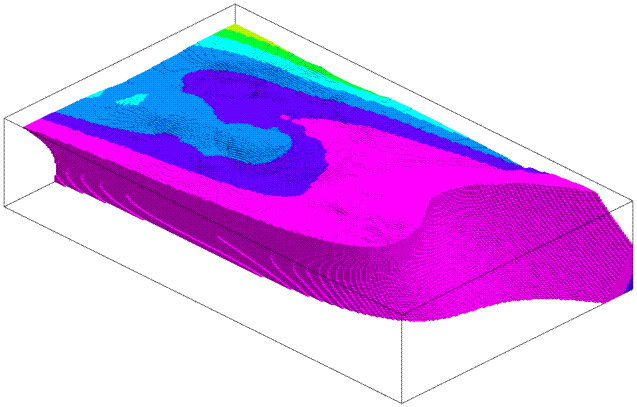
Figure 4. Third-Order 3D Trend Polynomial Model Showing Hydrothermal Gradients Based on Geochemistry
Enhancing Other Algorithms:
Polyenhancement is a process in which a polynomial is best-fit to XYZG data. The differences (residuals) between the original G-values and the G-values predicted by the polynomial are then modeled using any of the other RockWorks algorithms (e.g., Kriging). A solid based on the polynomial is then added to the residual model in order to create a final model. The net result is a model that is biased along the trend predicted by the polynomial but locally interpolated by the selected algorithm. The final model can also be constrained by the zero-level polynomial iso-shell.
The effects of polyenhancement are illustrated by a comparison of IDW-Isotropic modeling without and with polynomial enhancement and modeling with 2nd-order polyenhancement (Figure 5). In essence, the polynomial constrains the IDW interpolation to a reasonable interpretation.
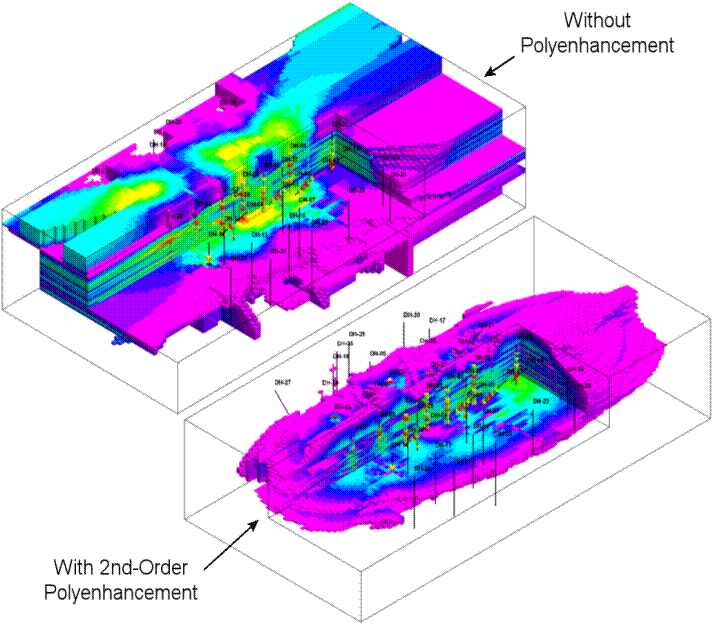
Figure 5. IDW Isotropic Modeling Without and with 2nd-Order Polyenhancement
3D Trend Polynomial Residuals
Subtracting the observed G-values from the predicted G-values can be a useful for tool from identifying bad or anomalous data. In other words, data that deviates from the trend. In Figure 6, the red blobs depict the highest residuals which is consistent with the variability within the central region. Notice, however that there are no red anomalies outside the central region.
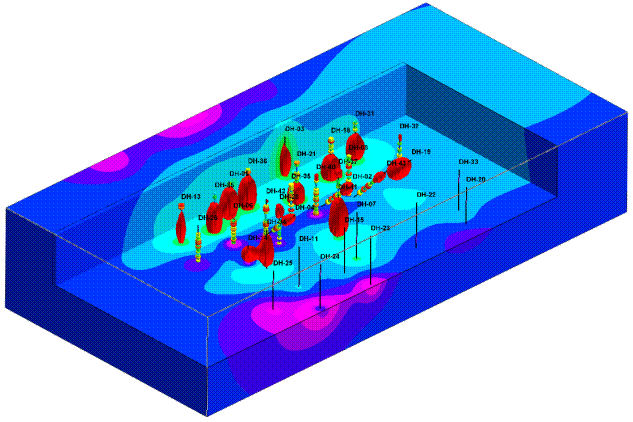
Figure 6. Isosurface Diagram Depicting 2nd-Order Polynomial Residuals
Polynomial residuals can also be used to evaluate the geological reasonableness of the polynomial itself. Ubiquitous large residuals are indicative of an unreasonable polynomial.
Limitations:
· If the XYZG data has no trend, 3D trend polynomial fitting may produce wildly erratic results.
· 3D trend polynomial modeling is currently limited to 2,000 points.
Guidelines
Before using the polyenhancement in combination within another algorithm, model the data with a trend polynomial first to see if there is, in fact, a spatial trend within the data. If the trend polynomial model doesn’t make geological sense, do not use the polyenhancement.